ทบทวนและอธิบายในรายวิชา IE221 ENGINEERING MATHEMATICS
จะมาอธิบายในหัวข้อ 3 หัวข้อด้วยกัน ประกอบไปด้วย
- ผลการแปลงลาปลาซ
LAPLACE TRANSFORM - การหารากของสมการด้วยวิธีนิวตัน-ราฟสัน
NEWTON-REPHSON METHOD - การแก้สมการเชิงเส้นด้วยวิธีการกำจัดแบบเกาส์
GAUSS ELIMINATION
ผลการแปลงลาปลาซ
LAPLACE TRANSFORM
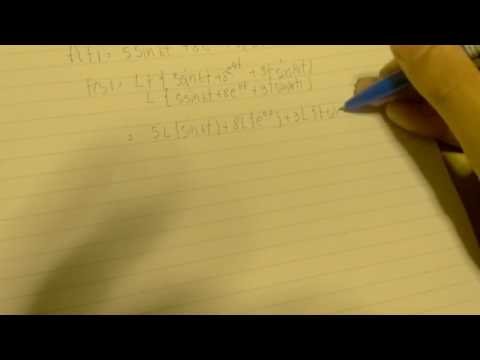
จากโจทย์ที่ได้ทำไปในคลิปวิดีโอนั้น โดยหลักของการแปลงลาปลาซนั้น เราสามารถทำได้ง่ายเพียงแค่แก้สมการปกติ โดยต้องดึงสัมประสิทธิ์ตัวหน้าออกมาก่อน แล้วต้องเปลี่ยนค่าในสมการ โดยสามารถดูค่าที่ต้องเปลี่ยนได้จากในตารางการเปลี่ยนเป็นลาปลาซ
 Loading...
Loading...
การหารากของสมการด้วยวิธีนิวตัน-ราฟสัน
NEWTON-REPHSON METHOD

ในโจทย์ข้อนี้นั้น โจทย์ได้กำหนด x1 = 3 มาแล้ว โดยที่โจทย์ต้องการให้เราหาค่าของสมการไปจนถึง X3 ขั้นแรกเราต้องหา f ‘(x) ก่อน โดยหาได้จากนำ f'(x) = -8 นั้น มาทำการดิฟ เราจำได้ f ‘(x) ออกมา ซึ่งค่าที่ได้มานี้ให้เรานำไปหารเพื่อให้เข้าสมการเพื่อหา X2 ดังนี้
xn+1 = xn − f(xn) / f ‘(xn)
แล้วทำการแก้สมการไปโดยการแทนค่า เปลี่ยนค่า n เมื่อเราต้องการทำในลำดับต่อๆไป
การแก้สมการเชิงเส้นด้วยวิธีการกำจัดแบบเกาส์
GAUSS ELIMINATION
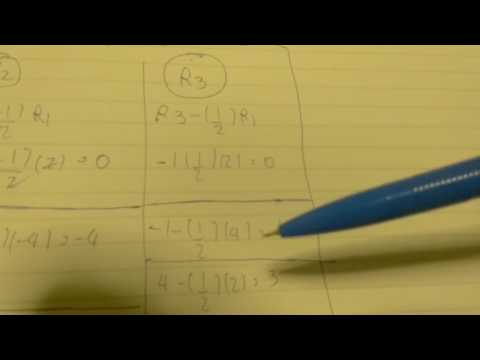
ในส่วนของการกำจัดแบบเกาส์นั้น เป็นวิธีหนึ่งในการแก้สมการเชิงเส้นที่ทำได้ง่าย ไม่ซับซ้อนมากนัก จากโจทย์ที่ให้มาในข้างต้น เราสามารถทำได้โดย นำสมการทั้งหมด มาแปลงเป็น เมทริกซ์ 3*3 เสร็จแล้วนำค่าของสมการใส่ลงไป โดยนำตัวสัมประสิทธิ์ ที่อยู่หน้า x ในลำดับต่างๆ เป็นค่าที่ต้องการใส่ในเมทริกซ์ เมื่อทำการใส่ค่าแล้วนั้น เราต้องเริ่มวิธีการกำจัดตัวเลขให้เป็น 0 ก่อน เริ่มทำที่แถวที่ 2 ในคอลัมน์ที่ 1 เราต้องนำค่าที่เหมือนกับตัวนั้น ลบ หรือ บวกออก แล้วเศษส่วนด้วยตัวเลขของแถว 1ด้านบน ทั้งหมดคูณด้วยตัวเลขที่อยู่ด้านบนถัดไป 1 แถวในคอลัมน์เดียวกัน ตัวถัดๆมาทำเหมือนกัน แต่เปลี่ยนตัวที่นำมาคูณเป็นตัวเลขที่อยู่ด้านบนของตัวนั้นๆ ทำไปจนหมดแถว พอหมดแถวแล้วให้ทำต่อในแถวที่ 3 ทำวิธีเดียวกันจนหมดแถว แล้วนำค่าทั้งหมดมาทำเป็น เมทริกซ์ใหม่ จะเห็นได้ว่ายังเหลือค่าที่แถวที่ 3 คอลัมน์ที่ 2 ทำเราต้องกำจัดอยู่ ทำโดยการใช้วิธีเดิม แต่เริ่มที่ตัวนี้ไม่ต้องเริ่มที่ตัวแรก ทำจนหมดบรรทัด คูณด้วยเลขที่อยู่แถวด้านบนแถวที่ 2 ได้เลย ไม่ต้องคูณที่แถว 1 เหมือนตอนแรก เสร็จแล้วจะได้เมทริกซ์ที่สมบูรณ์ เราจึงนำค่าที่ได้มาแปลงเป็นสมการ เพื่อหาค่าของ x1 , x2 , x3 ได้เลย
ทั้งหมดเป็นการสรุปเนื้อหาของวิชา engineering mathematics โดยที่เป็นการสรุปอย่างย่อๆ เพื่อให้เข้าใจได้ง่ายๆรวดเร็ว แนะนำดูคลิปวิธีการทำและลองทำความเข้าใจเป็นลำดับขั้นจะสามารถที่จะเข้าได้ไม่ยาก
ผู้เขียนบทความ
นาย สิรวิชญ์ รักชาติ รหัสนักศึกษา 1540902291