ENGINEERING MATHEMATICS
LAPLACE TRANSFORM
https://www.youtube.com/watch?v=lfYhd9hCi1Q&t=2s
ทฤษฎีและวิธีการหาลาปาซ
การแปลงลาปลาส Laplace transform คือการแปลงเชิงปริพันธ์ที่ใช้กันอย่างกว้างขวาง แสดงอยู่ในรูป {\displaystyle \displaystyle {\mathcal {L}}\left\{f(t)\right\}}{\displaystyle \displaystyle {\mathcal {L}}\left\{f(t)\right\}} การแปลงลาปลาสจะทำให้เกิดความเป็นเชิงเส้นของ f(t) ซึ่งค่า t เป็นอาร์กิวเมนต์จริง(t ≥ 0) จะแปลงไปอยู่ในรูปฟังก์ชัน F(s) โดย s เป็นอาร์กิวเมนต์เชิงซ้อน การแปลงนี้เป็นการทำฟังก์ชันหนึ่งต่อหนึ่งที่สำคัญมากในการใช้งานในทางปฏิบัติ คู่ฟังก์ชัน f(t) กับ F(s) นั้นจับคู่กันในตาราง การแปลงลาปลาสถูกใช้ประโยชน์จากคุณสมบัติที่มันมีความสัมพันธ์และการดำเนินการของฟังกันดังเดิม f(t) น้นสอดคล้องกับความสัมพันธ์กับการดำเนินการในรูปของ F(s) การแปลงลาปลาสถูกประยุกต์ใช้ในงานสำคัญมากมายที่เป็นแนวคิดทางวิทยาศาสตร์ สำหรับชื่อลาปลาสนี้มาจากชื่อของปีแยร์-ซีมง ลาปลาส ผู้ที่นำการแปลงนี้ไปใช้ในทฤษฎีความน่าจะเป็น
กำหนดให้ f(t) และ g(t) มีผลการแปลงลาปลาสเป็น F(s) และ G(s) ตามลำดับ:
{\displaystyle f(t)={\mathcal {L}}^{-1}\{F(s)\}}{\displaystyle f(t)={\mathcal {L}}^{-1}\{F(s)\}}
{\displaystyle g(t)={\mathcal {L}}^{-1}\{G(s)\}}{\displaystyle g(t)={\mathcal {L}}^{-1}\{G(s)\}}
F(t) คือ Time domain
F(s) คือ Laplace domain
โดยการใช้ตารางข้างล่างในการเปรียบเทียบ เทียบได้แล้วเราก็ใช้สูตรแปลงให้อยู่ในรูปลาปาซ
ใช้ความสามารถในการดูโจทย์ในการแทนค่า
Laplace transform แล้วก็มี Invers Laplace transform จะกลับกัน
สูตรตารางการแปลงลาปาซ
การแปลงลาปาซจะขึ้นอยู่จะหาค่าได้หรือไม่นั้นขึ้นอยู่กับค่าลิมิต ถ้าหาค่าได้เรากล่าวว่า คือการแปลงลาปาซในลู่เข้า แต่ถ้าหาค่าไม่ได้เรากล่าวว่า คือการแปลงลาปาซในลู่ออก
NEWTON-REPHSON METHOD
https://www.youtube.com/watch?v=RK3hqkUlCmw
ทบทวนการหารากของสมการด้วยวิธีนิวตัน-ราฟสัน NEWTON-REPHSON METHOD
สูตรการหารากสมการด้วยวิธีนิวตัน – ราฟสัน NEWTON-REPHSON METHOD
Xn + 1 = Xn – f ( Xn ) / f ‘( Xn )
ไม่ต้องหาช่วงเริ่มต้น แต่ต้องสมมติช่วงเริ่มต้นถ้าไม่ได้กำหนดมาให้ ของค่าเริ่มต้น X0 เพื่อไปหาค่าคำนวณของ X1 , X2 , X3 , X4 , X5 จากโจทย์จะกำหนดให้ซ้ำที่จุดทศนิยมเท่าไหร่
จากโจทย์ที่นำมาทบทวน คือ X0 = 1
ขั้นตอนที่ 1 เราต้องตั้งสมการขึ้นมาก่อน Xn + 1 = Xn – f ( Xn ) / f ‘( Xn ) แล้วแทนสูตรเข้าไป f ( Xn ) ส่วนล่างก็นำมาดิฟ f ‘( Xn )
ขั้นตอนที่ 2 กำหนดค่า X0 หาค่า X0 ได้ค่าไปแทน X1 , X2 , X3 ,X4 ,X5
ขั้นตอนที่ 3 แทนสมการไปจนกว่าจุดทศนิยมจะซ้ำกัน
LAGRANGE INTERPOLATION
https://www.youtube.com/watch?v=TuODe-09pEU
เราสามารถสร้างสมการ Lagrange Interpolation โดยทั่วไปเมื่อผ่าน N+1 f(x) = exact function
he Lagrange interpolating polynomial is the polynomial ![]() of degree
of degree ![]() that passes through the
that passes through the ![]() points
points ![]() ,
,![]() , …,
, …, ![]() , and is given by
, and is given by
|
(1)
|
where
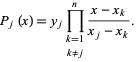 |
(2)
|
Written explicitly,
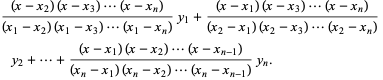 |
(3)
|
The formula was first published by Waring (1779), rediscovered by Euler in 1783, and published by Lagrange in 1795 (Jeffreys and Jeffreys 1988).
Lagrange interpolating polynomials are implemented in the Wolfram Language as InterpolatingPolynomial[data, var]. They are used, for example, in the construction of Newton-Cotes formulas.
When constructing interpolating polynomials, there is a tradeoff between having a better fit and having a smooth well-behaved fitting function. The more data points that are used in the interpolation, the higher the degree of the resulting polynomial, and therefore the greater oscillation it will exhibit between the data points. Therefore, a high-degree interpolation may be a poor predictor of the function between points, although the accuracy at the data points will be “perfect.”
For ![]() points,
points,
|
(4)
|
|||
|
(5)
|
Note that the function ![]() passes through the points
passes through the points ![]() , as can be seen for the case
, as can be seen for the case ![]() ,
,
|
(6)
|
|||
|
(7)
|
|||
|
(8)
|
Generalizing to arbitrary ![]() ,
,
|
(9)
|
The Lagrange interpolating polynomials can also be written using what Szegö (1975) called Lagrange’s fundamental interpolating polynomials. Let
|
(10)
|
|||
|
(11)
|
|||
|
(12)
|
|||
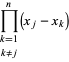 |
(13)
|
so that ![]() is an
is an ![]() th degree polynomial with zeros at
th degree polynomial with zeros at ![]() , …,
, …, ![]() . Then define the fundamental polynomials by
. Then define the fundamental polynomials by
|
(14)
|
which satisfy
|
(15)
|
where ![]() is the Kronecker delta. Now let
is the Kronecker delta. Now let ![]() , …,
, …, ![]() , then the expansion
, then the expansion
|
(16)
|
gives the unique Lagrange interpolating polynomial assuming the values ![]() at
at ![]() . More generally, let
. More generally, let ![]() be an arbitrary distribution on the interval
be an arbitrary distribution on the interval ![]() ,
, ![]() the associated orthogonal polynomials, and
the associated orthogonal polynomials, and ![]() , …,
, …, ![]() the fundamental polynomials corresponding to the set of zeros of a polynomial
the fundamental polynomials corresponding to the set of zeros of a polynomial ![]() . Then
. Then
|
(17)
|
for ![]() , 2, …,
, 2, …, ![]() , where
, where ![]() are Christoffel numbers.
are Christoffel numbers.
Lagrange interpolating polynomials give no error estimate. A more conceptually straightforward method for calculating them is Neville’s algorithm.